In diesem Artikel klären wir die folgende Frage: Welche Radumdrehung unserer Motoren ist notwendig, damit wir mit einem Roboter eine vorgegebene Strecke fahren können? Diese Radumdrehung können wir entweder durch Ausprobieren herausfinden oder ganz einfach und elegant über den Kreisumfang ausrechnen. Dafür brauchen wir nur ein paar Werte und etwas mathematisches Wissen und schon kann es losgehen.

Worum geht es genau?

Stellen wir uns folgendes vor: Du hast einen Roboter gebaut. Dieser Roboter hat Räder und fährt damit wie wild herum. Der Roboter könnte so aussehen auf den Fotos weiter unten. Nun haben wir folgenden Wunsch beziehungsweise  folgende Anforderung: Wir möchten gerne eine bestimmte Strecke fahren. Zum Beispiel 20 cm. Wie finden wir heraus, wie viele Umdrehungen der Motorachsen notwendig sind, damit wir diese Strecke zurücklegen können?

Eine Möglichkeit ist ausprobieren. Das hört sich vielleicht zu einfach an, aber wir mögen einfache Lösungen. Wenn es in eurem Fall okay ist, den Roboter einfach ein paar Mal fahren zu lassen, bis ihr herausgefunden habt, wie viele Umdrehungen für eine bestimmte Strecke notwendig sind, dann könnt ihr das gerne so machen.

Allerdings könnte es sein, dass ihr zum Beispiel keine Chance bekommt, euer Programm vorher einige Mal laufen zu lassen, um die Umdrehungen durch Testen herauszufinden. Vielleicht sollt ihr in eurem Programm nur an einer Stelle etwas ändern und es muss sofort funktionieren. Vielleicht möchtet ihr euer Programm aber auch so anpassen können, dass es für alle Rädergrößen funktioniert? In der zweiten Praktikumsaufgabe zu c4ev3 lautet die Aufgabe zum Beispiel, den Roboter 10 cm fahren zu lassen. Mit der in diesem Artikel vorgestellten Methode gelingt das ohne Probleme. Denn eines solltet ihr euch vor Augen führen: Die Strecke, die ihr mit eurem Roboter mit einer bestimmten Anzahl Umdrehungen der Motorachsen zurücklegen könnt, hängt von der Rädergröße ab. Glaubt ihr nicht? Dann lest einfach weiter.

Unterschiedliche Räder

LEGO® legt seinen Robotik-Sets verschiedene Räder bei. Bei der Education-Edition sind es zwei identische Räder wie auf den ersten beiden Bildern in der Galerie unter diesem Absatz zu sehen. In der Home-Edition sind es vier identische Räder, von denen zwei  auf  Bild 3 und 4 abgebildet sind. Zusätzlich gibt es noch die Möglichkeit, Räder wie auf dem fünften Bild zu bauen (in der Galerie unten vorblättern). Das geht in beiden Editionen. Die so gebauten Räder sind allerdings nicht sonderlich gut, weil sie kein Profil haben und nicht besonders breit sind.

Alle genannten Räder unterscheiden sich erheblich. Nicht nur in der Breite, die für uns in diesem Fall gar nicht wichtig ist, sondern vor allem im Radius und dadurch auch im Durchmesser. Das verändert natürlich den Umfang und der ist für uns sehr wichtig, wie wir im Folgenden noch sehen werden.

Die Radumdrehung über den Kreisumfang

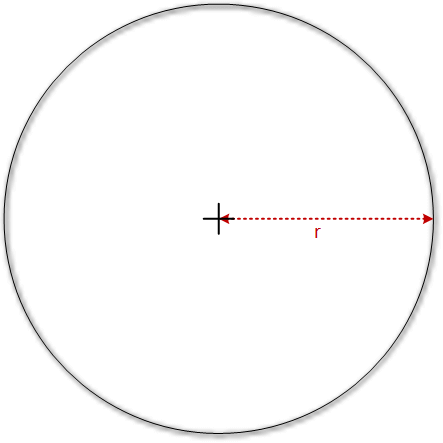
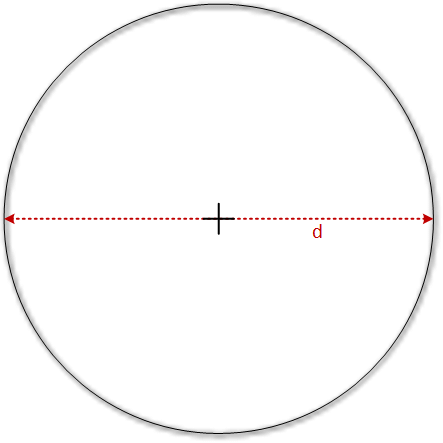
Wir brauchen nur einige wenige Werte, um berechnen zu können, wie oft sich unsere Motoren drehen müssen, um eine bestimmte Strecke zu fahren. Das Zauberwort heißt Kreisumfang. Wenn wir den Umfang eines Kreises wissen, dann sind wir ein ganzes Stück weiter. Der Kreisumfang lässt sich recht einfach berechnen. Wir brauchen entweder den Radius eines Kreises (im Bild unten links) oder den Durchmesser (im Bild unten rechts). Die beiden verschiedenen Formeln dafür sehen folgendermaßen aus:

Der Buchstabe U bezeichnet dem Umfang des Kreises. PI (π) ist die Kreiszahl, r der Radius und d der Durchmesser. Wie kommen wir an diese Werte? Zum Beispiel durch Messen. Ihr könnt ein Rad eures Roboters nehmen und mit einem Zollstock den Radius messen. Oder den Durchmesser, das ist euch überlassen.

Reifengröße bei LEGO®

LEGO® macht es uns aber noch einfacher. Wir können den Durchmesser auch einfach ablesen. Wenn ihr euch einen Reifen ganz genau anschaut, dann werdet ihr Angaben wie die folgenden darauf finden:

56 x 28 ZR

Was bedeutet das? Nun, der Durchmesser beträgt 56 mm und die Breite 28 mm. Oder in Zentimeter umgerechnet 5,6 cm Durchmesser und 2,8 cm Breite. ZR gibt die Bauart an. Damit haben wir die Werte, die wir brauchen. Wir verwenden im Folgenden den Durchmesser.

Die Berechnungen

Den Durchmessen durch zwei zu teilen, um den Radius zu bekommen, ist nämlich nicht sinnvoll. Wir nehmen die oben gezeigte Formel mit dem Durchmesser und können den Kreisumfang (weitere Infos) des Rads direkt berechnen. Aus praktischen Gründen haben wir den Wert für PI auf drei Nachkommastellen stark verkürzt. Für unsere Zwecke reicht das absolut aus.

Hilft uns das weiter? Aber klar doch. Wenn wir jetzt wissen, dass der Umfang 17,5895 cm ist und wir zum Beispiel 20 cm fahren wollen, dann können wir mit der folgenden Rechnung die gewünschten MotorumdrehungenM_{d} ausrechnen:

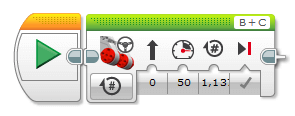
Unser Motor muss also 1,1370 Achsumdrehungen ausführen, damit wir mit den Rädern, die einen Durchmesser von 5,6 cm und einen Umfang von 17,5895 cm haben, 20 cm fahren können. Im Bild seht ihr die manuelle Ansteuerung zweier Motoren mit dem berechneten Wert. Die Umdrehungen sind leider nicht ganz sichtbar, da die LEGO®-Umgebung den Wert optisch abschneidet.

Wie ihr seht, kommen unter Umständen aber krumme Zahlen bei den Berechnungen heraus. Die können wir etwas runden. Zum Beispiel auf eine oder zwei Nachkommastellen. Für eine etwas genauere Motoransteuerung können wir statt kompletter Umdrehungen auch Gradzahlen angeben. Damit wird die Ansteuerung noch etwas besser. Dafür müssen wir aber den Wert, den wir oben berechnet haben, mit 360° multiplizieren.

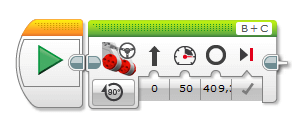
Der Grund ist, dass der berechnete Wert die Anzahl an Motorumdrehungen angibt. Also zum Beispiel 5, 2,34 oder 19 Umdrehungen. Wenn wir die Motoren aber in Grad ansteuern, bedeutet eine Umdrehung 360°, zwei Umdrehungen 720° (2 * 360°) und so weiter. Auf diese Weise können wir die Motoren noch etwas besser ansteuern. Die Berechnung der Motorumdrehung in Grad M_{g} sagt uns, dass sich die Achse unseres Motors um 409,32° drehen muss, um die gewünschten 20 cm zu fahren. Dieser Wert sollte wieder gerundet werden, da nur gerade Gradzahlen sinvoll sind. Die nachfolgende Abbildung zeigt die Ansteuerung der Motoren mit der berechneten Gradzahl. 

Mögliche Probleme

Im Allgemeinen funktionieren die gezeigten Berechnungen gut. Vor allem mit dem LEGO® Mindstorms® EV3, da dort die Motoren deutlich genauer angesteuert werden können, als das noch beim NXT der Fall war. Unsere Roboter lassen sich dadurch recht genau steuern.

Allerdings hängt die tatsächlich gefahrere Strecke nicht ausschließlich von unseren berechneten Werten ab – der klassische Unterschied zwischen Theorie und Praxis. In der Realität hängt die gefahrene Strecke auch davon ab, wie groß die Haftreibung ist, wie der Untergrund beschaffen ist, wie frisch/aufgeladen die Batterien beziehunweise Akkus sind. Nicht zuletzt hängt es auch etwas davon ab, mit wie viel Leistung wir die Motoren ansteuern. Je schneller der Roboter fährt, um so ungenauer wird die gefahrene Strecke. Das hängt damit zusammen, dass die LEGO®-Motoren nicht so genau wie reale Motoren sind.

Im Zweifel müsst ihr also wieder etwas probieren, wie gut die berechneten Strecke bei eurem Roboter mit der tatsächlich gefahrenen übereinstimmt.

Fazit

Mit den gezeigten Formeln sind wir jetzt in der Lage auszurechnen, wie viele Umdrehungen unsere Motoren machen müssen, um mit bestimmten Rädern eine vordefinierte Strecke zu fahren. Dafür brauchen wir nur den Kreisumfang und ein paar Informationen zu den Rädern unseres Roboters. Das ist in vielen Bereichen sehr nützlich.